ВЕРОЯТНОСТНЫЕ ХАРАКТЕРИСТИКИ НЕСУЩЕЙ СПОСОБНОСТИ

Аналогично большинству нагрузок несущую способность элементов конструкции ЛА в полете невозможно измерить. Опреде­ление ее вероятностных характеристик в стендовых условиях по результатам разрушающих испытаний сопряжено с большими ма­териальными затратами. Поэтому число разрушающих испытаний крайне ограничено, а следовательно, рассеивание статистических оценок искомых характеристик велико. Из этого. следует, что основным является расчетно-статистический метод косвенного опре­деления вероятностных характеристик несущей способности по ана­литической детерминированной модели зависимости ее от возму­щений (модели напряженно-деформированного состояния конструк­ции) и известным вероятностным характеристикам возмущающих параметров.

В силу специфических особенностей конструкции различных элементов и их нагружения весьма разнообразны модели напряжен­но-деформированного состояния. Заметим, что при статическом на­гружении в модель обычно включают уравнения равновесия, свя­зывающие напряжение с действующими нагрузками и перемеще­ниями, зависимости между напряжениями и деформациями, а также геометрические соотношения деформаций и перемещений. Естественно, что надежность конструкции может быть определена расчетно-статистическим методом лишь по той или иной теории прочности с введением соответствующего критерия (эквивалентного напряжения).

Рассмотрим возмущающие параметры несущей способности кон­струкции. К ним относятся физико-механические характеристики конструкционных материалов (предел прочности ств, предел текуче­сти от, модуль упругости Е, коэффициент Пуассона р и др.) и раз­меры конструкции (диаметры и длины отсеков, толщины обшивки, полок и стенок профилей силового набора и т. п.). Случайная при­рода этих параметров обусловлена в основном погрешностями про­изводства: неоднородностью материала, допусками на изготовле­ние, несовершенством технологических процессов (например штам­повки). Физико-механические характеристики материалов, а строго говоря, и размеры зависят от температуры. В свою очередь темпе­ратурное поле конструкции в общем случае переменно во времени и случайно.

При фиксированной температуре указанные возмущающие па­раметры — случайные величины. Статистическая обработка боль­шого числа опытных данных показывает, что их распределение близко к нормальному, хотя и отлично от него главным образом по­тому, что параметры несущей способности конструкции по физиче­скому смыслу не могут быть отрицательными. На практике часто принимают гипотезу о нормальном распределении параметров не­сущей способности и лишь иногда аппроксимируют эмпирические распределения логарифмически нормальным, усеченным нормаль­ным и другими законами.

В табл. 9 приложения приведены значения математического ожидания т и коэффициента вариации v пределов прочности ов и текучести от некоторых авиационных материалов [14]; кроме того, указаны номинальная толщина листав 6Ном и объем выборки п, по которой оценены этй характеристики. Для сплава АМгб эти значе­ния даны также в зависимости от ширины Ъ листов. Аналогичные вероятностные характеристики толщины листов б даны в табл. 10 приложения В зависимости ОТ номинальных ТОЛЩИНЫ бном и ширины ЬЕ0М листов. Большие размеры элементов конструкции, такие как диаметр и длина отсека, в силу относительной малости назначае­мых на них производственных допусков, как правило, можно счи­тать неслучайными параметрами в отличие от толщины б. По моду­лям упругости и коэффициентам Пуассона в настоящее время, к со­жалению, в известной нам литературе не имеется статистических данных. Из рассмотрения табл. 9 и 10 приложения следует,-что ко­эффициенты вариации параметров, определяющих несущую способ­ность металлических конструкций ЛА, в основном не превышают 10—12%. Неметаллические конструкционные материалы, например стеклопластики, обладают большим разбросом механических ха­рактеристик.

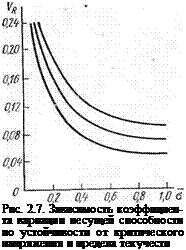
Практика показывает, что разброс несущей способности конст­рукции в целом может оказаться весьма значительным. Это, в част­ности, имеет место для неподкрепленных оболочек с большим отно­шением радиуса кривизны к толщине и для сварных конструкций со значительным числом швов. На рис. 2.7 изображена зависимость коэффициента вариации vR несущей способности по устойчивости от отношения і-=УИ[акр]/.М[аТс:ж] математических ожиданий кри­тического напряжения о„р и предела текучести при сжатии °Т сж некоторых, типичных для корпуса ракеты, элементов конструкции, подвергающихся сжатию [7-1]. Из рисунка видно, что и в этом случае разброс несущей способности может быть значительным (коэффи­циент вариации Vr=5ч-24%).

Температурное воздействие удобно учитывать в модели несущей
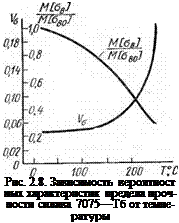
способности «полуслучайной» функцией, вводя в рассмотрение за­висимости математического ожидания и коэффициента вариации механических характеристик конструкционных материалов от тем­пературы. В качестве примера на рис. 2.8 приведены зависимости математического ожидания Л4[ов] и коэффициента вариации va предела прочности на растяжение алюминиевого сплава 7075—Тб от температуры Т, причем значения Л1[ов] отнесены к номинально­му пределу прочности Мово] ПРИ 0°С [71]. Такие зависимости можно аппроксимировать различными аналитическими выражения­ми. Например, зависимость предела прочности некоторых материа­лов от температуры [51]

°в(7’)=—0воехР[-а(7’-*)21’ (2-2°)

где а и b — статистические коэффициенты (для данного материа­ла). В частности, для алюминиевого сплава Д16АТ величины

а=6,25-10~6 град~2, Ь=0°С; для стали ЗОХГСА
а= 11,75-10-6 град-2, ь=т при 7^300 С и 6=300°С
при Т>300° С.

Вероятностные характеристики теплофизических параметров конструкционных материалов в известной нам литературе не при­ведены. Ориентировочно можно полагать предельные отклонения теплоемкости и теплопроводности материалов равными 10% [4].

При длительном нагружении конструкции на первый план вы­ступает проблема долговечности, количественные характеристики которой зависят от распределения случайного времени т до разру-

Таблица 2.1

шения. На величину т существенно влияют температура Т и уро­вень Од действующих напряжений. В табл, 2.1 приведены значения логарифма среднего времени до разрушения lgrcp и среднего квад­ратического отклонения cflgT] сплава ЭП109ВД на никелевой осно­ве и стали ЭИ961 — жаропрочных материалов, применяемых для изготовления газотурбинных двигателей {45].

Из таблицы видно, что повышение температуры и напряжения вызывает увеличение разброса времени т.

В условиях длительного нагружения ^нагр при высоких темпера­турах заметна ползучесть конструкционных материалов. В табл. 2.2 приведены значения вероятностных характеристик ползучести рас­смотренных выше жаропрочных материалов: математическое ожи­дание тг и среднее квадратическое отклонение ов остаточной де­формации {45].

Таблица 2.2 Материал Т, град Одіо—7, Н мг *Н>Гр> 4 m~ % °£» % ЭП109ВД 900 19 100 0,123 0,130 6 1000 0,237 0,057 ЭИ961 500 34 100 0,185 0,058 28 1000 0,199 0,043

Несущая способность конструкции в условиях знакопеременного циклического нагружения характеризуется функциями выносливо­сти (кривыми усталости): зависимостью a_i = a_,(Л’) предела вы­носливости а і от числа циклов или зависимостью N=N(zm) разру­шающего числа циклов N от амплитуды гт напряжения. По приро­де кривые усталости являются случайными функциями. Если полагать распределение числа циклов N при фиксированном значе­нии Zm известным (например, нормальным) и рассматривать функ­цию N=N(zm) как «полуслучайную», то достаточными вероятност­ными характеристиками несущей способности будут зависимости логарифма среднего значения разрушающего числа циклов lgjV и среднего квадратического отклонения o[lg Л/] или коэффициента ва­риации % n от амплитуды Zm, На указанные характеристики влия­ют температура, достояние поверхности образцов и другие факто­ры. Значения IgA» и ;o{lgЛ] для некоторых конструкционных мате­риалов приведены в табл. 11 приложения {17, 44].

Установлено, что для ряда алюминиевых деформируемых спла­вов (В95, Діб, АВ, АДЗЗ и др.) существует единая кривая устало­сти в относительных координатах [45]:

p[lg(A^+7V0)]-“, (2.21)

ГДЄ z — отношение амплитуды zm К пределу ВЫНОСЛИВОСТИ 0_! на базе 107 циклов; "o_i — отношение o“i при N—*oo к a_i при N— = 107 (в_1=0,47); р = 38,0; N0^(l — У 5)- Ю3; а=2,1 — параметры кривой.

Функцию (2.21) нетрудно представить в виде A=A(zm). Преоб­разовав ее, получим

jV —ехр {2,3 [Р3—i/(^m °—1)]1,к}-No. (2.22)

На рис. 2.9 показана кривая усталости в относительных коор­динатах для сплава АВ при ста­ционарном нагружении [45].

Наличие единой кривой уста­лости облегчает задачу, так как для* определения выносливости материала при любом числе цик-

Рис. 2.9. Кривая усталости сплава АВ

лов оказывается достаточным найти по результатам испытаний образцов из данного материала значение лишь при А=107.

Из характеристик рассеивания усталостных свойств (средних квадратических отклонений и коэффициентов вариации величин G-і и IgA) наиболее стабильным является, практически не за­висящий от базы испытаний (числа циклов нагружения). Напри­мер, для сплава АВ в среднем ‘Ho_1=0,06. Коэффициент вариации предела выносливости и параметры кривой усталости полностью определяют зависимость вероятностных характеристик разрушаю­щего числа циклов N от амплитуды напряжений zm. Среднее зна­чение (математическое ожидание) IgA можно найти по зависимо­сти (2.22), а коэффициент вариации

^"=лг[‘+^г (1вЛТ,"Ь {2-23)

где 6=^1.

На рис. 2.10 показаны сплошной линией расчетная (2.23), а пунк­тирной — экспериментальная зависимости среднего квадратическо­го отклонения o[lgA^] от среднего значения IgA для сплава АВ [45]. Как видно по рисунку, совпадение данных вполне удовлетворитель­ное. Исследованиями [17, 45] установлено, что масштабный фактор и концентрация напряжений оказывают влияние на характеристи­ки выносливости, причем в качестве критерия подобия можно при­нимать величину L/G отношения периметра образца (детали) к гра­диенту напряжений. На рис. 2.11 приведены зависимости предела

выносливости °!U на базе 107 циклов (сплошные прямые) и его среднего квадратического отклонения (пунктирные пря­

мые) от величины lg(L/G) для сплавов АВ (прямые 1), ВМ65-1 (прямые 2) и МЛ5 (прямые 3) при стационарном нагружений [45].

§ 2.4. ИНЖЕНЕРНЫЕ МЕТОДЫ РАСЧЕТА НАДЕЖНОСТИ

КОНСТРУКЦИИ

Применим методы, изложенные в гл. I, для расчета на­дежности элементов конструкции ЛА, ограничиваясь случаем одно­го возможного предельного состояния. Как отмечалось в § 2.1, за­дача существенно упрощается, если пренебречь различием напря­женно-деформированного состояния в разных точках конструкции. Но в этом случае рассчитывать надежность следует применительно к «слабейшей» точке, в которой состояние конструкции наиболее близко к предельному. Поскольку в остальных точках вероятность разрушения меньше, чем в «слабейшей», т. е. в них имеется неко­торый «запас по надежности», конструкция излишне утяжеляется. Кроме того, расчет надежности в общей пространственно-времен­ной постановке — чрезвычайно трудоемкая задача.

Поэтому для практики приемлемо обеспечивать равнонадеж — ность конструкции методом последовательных приближений: опре­делять вероятность неразрушения не только в «слабейшей», но и в других характерных точках конструкции, уравнивать запас по на­дежности в них изменением геометрических параметров конструк­ции, например толщины стенки, и повторять затем расчет вероятно­сти неразрушения. «Слабейшую» точку можно выявить детермини­рованным прочностным расчетом при допущениях, указанных в § 2.1 для выбора расчетного случая. При таком подходе достаточно рассматривать нагрузку и несущую способность как случайные про­цессы. Будем считать пересечения реализаций нагрузки S(t) и не-

3—1218

сущей способности R(t) редкими случайными событиями, а распре­деление реализаций в каждом сечении t=tj — нормальным.

Применение нормального закона оправдано тем, что в случае совместного действия достаточно большого числа случайных возму­щений, подчиняющихся различным законам распределения, если среди них нет превалирующего, результирующее возмущающее воз­действие имеет, согласно центральной предельной теореме теории вероятностей, распределение, близкое к нормальному. На практике распределения многих возмущений отличны от нормального хотя бы потому, что по физическому смыслу целый ряд параметров (пре­дел прочности, толщина и т. п.) не могут быть отрицательными. Но усечения распределений обычно невелики, что позволяет игнориро­вать теоретическую нестрогоеть допущения нормального распреде­ления.

Для того чтобы использовать изложенный в § 1.4 математиче­ский аппарат, оперируя с положительными выбросами, введем вза­мен параметра состояния Z(t), определяемого равенством (2.1), параметр

U{t)=S{t) — R{t). (2.24)

Тогда определение вероятности пересечения реализаций нагрузки и несущей способности сводится к задаче о положительном выбросе функции V(f) за нулевой уровень.

Элементы конструкции в зависимости от их динамических свойств по-разному сопротивляются кратковременным нагрузкам. Нередко импульсное нагружение не вызывает разрушения, тогда как нагрузка такой же величины, приложенная статически, разру­шает конструкцию. Из этого следует необходимость учета длитель­ности выбросов, так как в противном случае сильно завышается ве­роятность разрушения и соответственно вес конструкции.

Пусть ткр — критическая длительность выброса, т. е. разруше­ние имеет место при т>ткр. Найдем вероятность того, что длитель­ность выброса превысит критическую. Исследованиями [37, 56] уста­новлено, что с возрастанием уровня, выбросы за который означают отказ, длительность выбросов т уменьшается, а закон /(т) ее рас­пределения стремится к закону Релея

•

/{%)=— e-*V(2a*). (2.25)

о 2

Параметр о нетрудно определить по средней длительности выброса т, учитывая, что для этого распределения математическое ожидание

УИ[т]=т=|Ая7І2о." (2.26)

Средняя длительность выброса в общем ‘случае определяется выражением (1.53); в случае стационарного случайного процес­са— выражением (1,55), а в случае нормального стационарного

процесса — выражением (1.58) или (1.64). При фиксированном зна­чении Ткр с учетом выражения (2.26) искомая вероятность

=вер {г >ткр) = J f{x)dx=e~T^{A, (2.27)

ткр

При более строгом подходе следует учесть, что в силу стохасти­ческой природы сопротивляемости конструкции импульсным на­грузкам Ткр является случайной величиной. Пусть известна плот­ность /(ткр) ее распределения. Разобьем область возможных значе­ний Ткр на п интервалов. Введем в рассмотрение гипотезу Ни состоящую в том, что значение Ткр находится в i-u интервале [ткр й Ткр »4-С? Ткр]. Вероятность этой гипотезы

P{Hi)=f{^i)dxKV.

Обозначим через Р(А/Ні) условную вероятность того, что т>Ткр* при условии, что имеет место гипотеза Ни Вероятность Р(А/Ні) оп­ределяют выражением (2.27) с заменой в нем Ткр на Ткр». По фор­муле полной вероятности,

Р—~ І Р (A/HJPiHi).

i-i

Полагая, что величина йткр мала (число интервалов выбрано доста­точно большим) и переходя на этом основании от суммирования к интегрированию, получим

р,=] е“^р/(4та) / (ткр) С1ХКР. (2.28)

о

На практике пределы интегрирования можно заменить величи­нами а>0 и Ь<оо, исходя из диапазона реальных значений ткр.

По принятой в теории выбросов методике, если время Т функ­ционирования конструкции стремится к нулю, то вероятность от­сутствия выбросов становится сколь угодно близкой к единице не­зависимо от вероятностных характеристик нагрузки и несущей спо­собности в начальный момент времени. Поэтому введем в рассмот­рение начальную надежность Р(0) как вероятность неразрушения в квазистатич’еской постановке в момент /=0. Общую вероятность неразрушения Р(Т) определим как произведение начальной надеж­ности на условную вероятность отсутствия выбросов длительностью, большей тКр на интервале [0, 7], вычисленную при условии, что в на­чальный момент времени разрушение не наступает, т. е.

Я(7’)=Я(0){1— [1—ЛСП]^Ь (2.29)

где Р (Т) =Bep{t/(tf) <iO/t^T}—вероятность отсутствия выбро­сов, определяемая при принятых допущениях зависимостью (1.69) в общем случае или зависимостью (1.70) при стационарных нор­мальных процессах.

3*

Среднее число выбросов п в единицу времени, необходимое для расчета вероятности Р (Т), определяют в общем случае выражения­ми (1.49), (1.50), для стационарного процесса U(t) —выражением (1.54), а для нормального стационарного процесса — выражением (1.57) или (1.63) с учетом того, что рассматривают выбросы за ну­левой уровень. При нормальном распределении реализаций можно получить в конечном виде и для нестационарного процесса выраже­ние среднего числа выбросов в единицу времени.

Подставим в (1.49) выражение плотности совместного распреде­ления ординаты U(t) нормального случайного процесса и скорости V (t) ее изменения:

Из соотношения И(/) =——- U (t) следует, что

dt

« … «W*»

mvW=~rr muV)’

at

Можно показать также [49], что

1 ‘ дки(іг tt)

au (^) °v 0/) dtl

Обозначим внутренний интеграл (1.49) через по, подчеркивая ин­дексом «0», что рассматриваются выбросы за нулевой уровень. Тогда получим

.. 1 Г ти mv 1

где Мх=— ~ —1— r„v-1——

V-rlv L V J

Из выражений (2.30)-f-(2.32) видно, что no=m(t)—перемен­ное во времени значение среднего числа выбросов в единицу вре­мени. Полагая выбросы редкими событиями и зная функцию m(t), нетрудно определить вероятность

Таким образом, для расчета вероятности Р{Т) необходимо знать математическое ожидание

mv (2.34)

л корреляционную функцию

К и [tj, ti)—Ks(tj, ti) 2 K#s{tj’ (2.35)

t. e. математические ожидания нагрузки ms(t) и несущей способно­сти mR(t), их автокорреляционные функции Ks(k> к), к), а

также корреляционную функцию связи Krs^u к).

Аналитическое выражение вероятности {2.33) для нестационар­ного процесса U(t) в виде, приемлемом для инженерной практики, не удается получить. Можно указать следующие пути приближен­ного решения этой задачи. Если принять математические ожидания и дисперсии случайных процессов U(t) я V(/) в выражении (2,32) их максимальными значениями и пренебречь корреляцией между процессом U(t) и скоростью V(/) его измёйения, то величина m становится не зависящей от времени и вероятность Pi(T) опреде­ляется простым выражением (1.71). Указанные здесь допущения приводят к некоторому занижению вероятности Р(Т)-

Сущность другого упрощения заключается в представлении не­стационарного случайного процесса U(t) в виде суммы некоррели­рованных стационарных случайных процессов Wi(t), взятых со спе­циальным образом подобранными неслучайными коэффициентами <Рг(/)- В основу такого представления можно положить принцип, ис­пользуемый для канонического разложения случайных процессов. Условие неразрушения U(t)<Z0 заменяют в этом случае более же­стким условием: считают, что отказ имеет место при выбросе за ну­левой уровень хотя бы одной из составляющих функции U{t). Идея упрощения состоит в том, что нестационарность процесса сосредо­точивается в неслучайных функциях времени.

Стремление к рассмотрению случайного процесса U(t) как ста­ционарного (если это допустимо) вполне естественно, так как в этом случае вероятность Pt (Т) определяется весьма простым выражени­ем (1.70), которое можно представить в виде

( т V	Г <*%(*) 1 — тУ(2°і)
1 2я ‘	[_ йгЪ J t=o У

PjS^exp

, (2.36)

где си2 и ргг(т) — соответственно дисперсия и нормированная кор­реляционная функция случайного процесса U (/).

На основании равенств (1.59) и (2.35)

au^as+°l-2asaRrsti (2.37)

Р рМ — 2 l°sP з С*) ~Ь а%Рл(т) ~ 2asoRp s/г СО ]» (2- 38)

°и

где о2 и о2 — дисперсии нагрузки и несущей способности; р8(т), Рн(т), ряи(т) —нормированные автокорреляционные функции и
нормированная корреляционная функция связи случайных процес­сов S(t) и R(t) rSR=psR(0) —коэффициент корреляции величин 5 и R в одном <и том же сечении.

Рассмотрим постановку задачи (2.9), т. е. случай стабильности вероятностных характеристик несущей способности во времени, по­лагая, что нагрузка S (/) и несущая способность R не коррелирова — ны. Из выражения (2.36) находим, что

Можно убедиться в том, что выражение (2.39) дает нижнюю» границу значений вероятности Р. Более корректным следует счи­тать представление вероятности Р в соответствии с формулой пол­ной вероятности в виде суммы произведений вероятностей нахожде­ния уровней несущей способности в интервалах [R, R+dR] на веро­ятности выброса реализаций нагрузки за эти уровни, т. е. в пределе

Pt=$f(R)e-n«TdR, (2.40)

о

где f(R) — плотность распределения несущей способности; nR — среднее число выбросов функции S(t) за уровень R, определяемое выражением (1.63).

Выражение (2.40) справедливо не только при нормальном, но и при других распределениях. Если f(R) —плотность нормального распределения, то, полагая и разложив в степенной ряд

экспоненциальный множитель под интегралом (2.40), удается полу­чить приближенное аналитическое выражение вероятности

где А — параметр, определенный выражением (1.65).

В расчетах надежности конструкций удобно пользоваться без­размерными параметрами: средним коэффициентом запаса

r=mRlms (2.42)

и коэффициентами вариации

(2.43)

(4-І)2

/424

В квазистатической постановке задачи при использовании раз­ностного параметра состояния (2.1) в соответствии с выражением (1.37) вероятность неразрушения

где mR и ms — математические ожидания несущей способности и нагрузки.

В безразмерных параметрах (2.42), (2.43), при некоррелирован­ности нагрузки и несущей способности

Р—Ф [(т|— 1)//’+V*]. (2.46)

По зависимости (2.45) определяют, в частности, начальную надеж­ность Р(0), учитываемую в (2.29),

Пример. Рассчитать вероятность неразрушения трубопровода диаметром d— = 50±0,3 мм, имеющего номинальную толщину стенки 6ПОм = 1,5 мм, выполнен­ного из стали Х18Н10Т и нагруженного внутренним избыточным давлением З — 107 Н/м2 с допуском ±15%.

Решение. Предположим, что предел прочности 0в, толщина стенки 6 и на­грузка S распределены по нормальному закону, а предельные отклонения равны трем средним квадратическим отклонениям, т. е. оа=Дй/3=0,3/3=0,1 мм; os= =AS/3=3- 107-0,15/3=0,15-107 Н/м2.

В качестве математических ожиданий диаметра d и давления S примем но­минальные значения этих параметров. Из табл. 9 и 10 приложения находим ма­тематические ожидания: та =63,73-9,81 • 105 Н/м2 и т6 =1,54 мм; коэффициенты вариации предела прочности и толщины va— 5,65%; иг=3,38%. Коэффициент ва­риации диаметра Od=0d/f«d=O,1/50=0,002=0,2%.

Поскольку нагрузкой яівляется рабочее давление, примем в качестве несущей способности R разрушающее давление, которое, как известно из теории безмо — ментных оболочек, в данном случае определяют выражением R = 2св5/<±

Подставляя в него математические ожидания возмущающих параметров, на­ходим математическое ожидание несущей способности:

2т т, 2-63,73-1,5

тп =———- — =——————- 9,81-106 = 3,75-107Н/Ы2.

к та 50

Зависимость несущей способности от возмущающих параметров, приведенная выше, имеет вид (L105). Поэтому, согласно зависимости (1.106), коэффициент ва­риации несущей способности

vR = /r^a+vl+v‘^ = V 5,652 + 3,382 + 0,22 = 6,59%.

В данном примере диаметр можно считать неслучайной величиной, так как его относительный разброс существенно меньше разброса предела прочности и толщины.

По зависимости (2.45) и табл. 3 ‘приложения с учетом того, что rRS=0, ве­роятность неразрушения

= Ф (2,6) = 0,995339.

Если закон распределения параметра состояния конструкции отличается от нормального, то можно воспользоваться для вычис­ления вероятности неразрушения одним из приближенных методов (см. § 1.4), например разложением Шарлье (1.40), либо проинте­грировать численным методом плотность распределения параметра состояния.

При проектировании ЛА значительно легче получить в качест­ве исходных данных математические ожидания и дисперсии (или коэффициенты вариации) нагрузки и несущей способности, нежели корреляцонные функции. Это существенно ограничивает возмож­ность использования даже изложенных выше простейших методов, основанных на математическом аппарате теории выбросов случай­ных функций, и дает преимущества квазистатической постановке задачи. Зачастую нельзя пренебрегать изменениями нагрузки и не­сущей способности во времени. В ряде случаев реализации случай­ных процессов S(t) и R{t) не перемешиваются, а имеют характер пучка эквидистантных кривых, параллельных или расходящихся прямых. В этих условиях удобно представлять нагрузку и несущую способность «полуслучайными» функциями времени. «Полуслучай — ные» функции широко (используются, в частности, для описания про­цессов износа и старения конструкций [19, 25].

Параметр состояния конструкции как «полуслучайную» функ­цию можно представить в общем случае выражением

Z(t)=Ot(t)+H, (2.47)

где G и Н—случайные величины; <р(£) — неслучайная функция времени. .

Математическое ожидание mz(t) и дисперсию oz2(t) находят методом линеаризации [см. зависимости (1.101), (1.102)] по матема­тическим ожиданиям, дисперсиям и коэффициенту корреляции ве­личин G и Я. Вероятность неразрушения при нормальном распре­делении рассчитывают, как и в квазистатической постановке, по зависимости (2.45), но для нескольких моментов времени. Можно также заранее выявить расчетный (наиболее опасный) момент вре-

=0.

В случае нескольких возможных предельных состояний следу­ет воспользоваться для расчета вероятности неразрушения общими методами, указанными в § 1.4, в частности при двух нормально рас­пределенных параметрах состояния — зависимостью (1.41). Пред­варительно определяют методом линеаризации математические ожидания, дисперсии и коэффициент корреляции параметров со­стояния по соответствующим характеристикам нагрузок и несущих способностей, а последние в свою очередь — по вероятностным ха­рактеристикам возмущений. Так, при двух разностных параметрах состояния U и U2 на основании теорем о математическом ожида­нии и дисперсии линейной функции и определения корреляционно­го момента:

mu,=’nRi mSi»

°t/, — °tfi “b °Si “ 2ГЯ.«і0Л1°51 ;

°?/г=4, “Г °l,— 2r*>s. e/?.°s.;

Г*А0Л“ rftAVr/?AVsJ — где /n;, 32, Гу, (/, y=f/lt */2, /?„ /?2. ^1 52)—соответственно матема­тические Ожидания, дисперсии и коэффициенты корреляции пара­метров состояния, несущих способностей и нагрузок. Надежность конструкций ЛА обычно бывает достаточно высока, что дает осно­вание считать предельные состояния некоррелированными и исполь­зовать зависимость вида (1-42).